Greatest Common Factor (GCF) Chart (1-100)
GCF Chart (1-100)
| Number | GCF |
|---|
The Greatest Common Factor Chart 1-100 Explained
The greatest common factor (GCF) is the largest integer that divides two or more numbers without leaving a remainder. Understanding the greatest common factor chart 1-100 is essential for various applications in mathematics, particularly in simplifying fractions and solving problems related to least common multiples.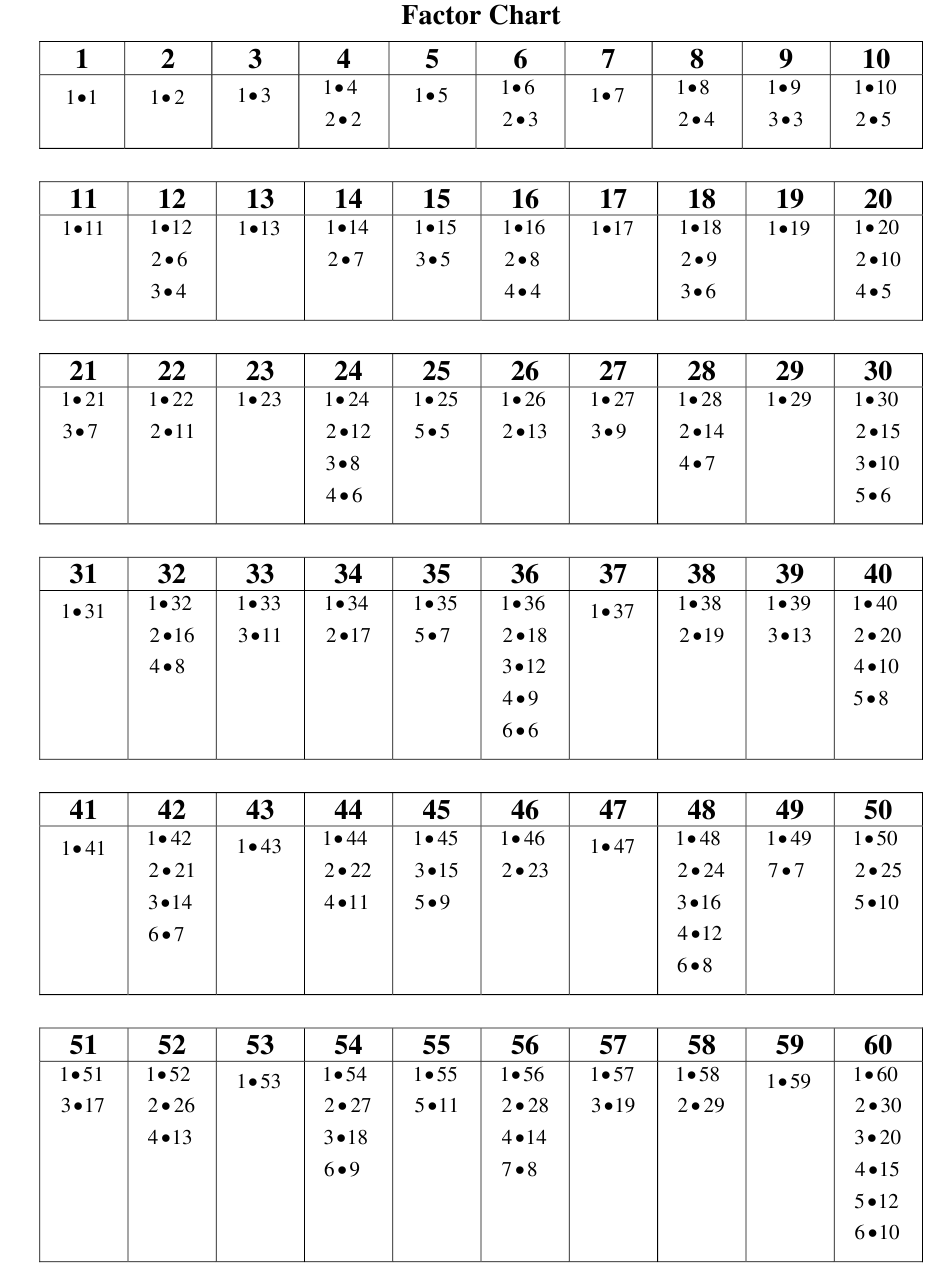
How to Use the Greatest Common Factor Chart 1-100
A greatest common factor chart 1-100 helps to quickly identify the GCF of any two numbers between 1 and 100. Here’s how it works:
- Locate the two numbers for which you want to find the GCF.
- Identify their common factors from the chart.
- The largest number listed is the GCF.
Benefits of Using a GCF Chart
Employing a GCF chart can streamline your calculations. Here are several benefits:
- Improves speed in problem-solving.
- Minimizes errors in mathematical operations.
- Assists in fraction simplification.
Common Mistakes When Using GCF Charts
While using the greatest common factor chart 1-100, users may encounter common pitfalls:
- Neglecting to check all common factors.
- Assuming the largest number in the set is always the GCF.
What to Do Next
After mastering the greatest common factor chart 1-100, it’s beneficial to practice with different sets of numbers. This reinforcement helps solidify your grasp on the concept and its applications.
10 Key Facts About Greatest Common Factor Chart 1-100
- How do you greatest common factor chart 1-100? You analyze the chart to find the largest common divisor for your chosen numbers.
- Can you easily greatest common factor chart 1-100? Yes, especially if you follow the step-by-step method outlined in this guide.
- Is a GCF chart applicable beyond 100? Absolutely, the concept can be applied to any set of integers.
- Why use a GCF chart? It simplifies the process of finding common factors efficiently.
- Can technology aid in finding GCF? Yes, various calculators and online tools can assist.
- Is it essential for fraction simplification? Yes, knowledge of the GCF is vital for reducing fractions.
- Are there exceptions using GCF? Only when numbers are prime; their GCF is always 1.
- How does GCF relate to LCM? They are interrelated; the product of the GCF and LCM equals the product of the two numbers.
- What’s an example of GCF from 1-100? The GCF of 36 and 60 is 12.
- Is practice important for GCF calculation? Yes, regular practice ensures a better understanding and quicker recall.
Wow, this chart is so helpful! I always get confused with factors, and now I can finally figure them out easier. Thanks for sharing! 🙌
Thanks for this! I’ve been struggling with math lately, and this GCF chart might actually make it a bit easier for me. Do you have similar resources for primes?